Fillet Weld Legs Determine Size and Throat of Fillet Welds Fillet weld sizes determine theoretical throat. The product of the size and cos45°in case where an isosceles right triangle may inscribe within the fillet weld cross section:S×cos45°= 0.7S, as shown in Fig. 2 － How to calculate theoretical throat. The throat thickness bisects the isosceles triangle, splitting the single triangle into two right triangles with the throat thickness on one side and the leg of the fillet weld being the hypotenuse. Thus the leg of the fillet weld is found to be L = T/COS(45) or as commonly approximated L= T/(0.7). Given: Weld throat thickness = 8.2 mm. Formula: Weld size (h) = t √2 - ( It is the relation between weld size and weld throat thickness) Solution: weld size (h) = t √2. Weld size (h) = 11.59 mm. The effective area of a weld is calculated by multiplying the length of the weld times the throat of the weld. For design purposes we use the theoretical throat as shown below. In the above diagram, is the fillet weld leg size. The theoretical throat is calculated. Video 5 Dimension of the complete fillet weld 1) size of the fillet weld 2) length of the fillet weld 3) pitch of the fillet weld 4) chain intermittent fille.

• Fillet Weld Effective Throat
• Weld Throat Thickness Calculation

Unless you are a design engineer you typically don’t have to worry about determining the strength of a weld. The strength of a weld refers to its load carrying capacity, or how much load it can handle before it fails. However, it is very important for all of us involved in the welding process, from welders to production supervisors to quality personnel and welding engineers to understand the basics of weld design.

Overwelding is an epidemic in our industry. This stems from not really understanding how to properly size a weld. But even companies with teams of engineers, having the luxury of using finite element analysis software, still call for weld sizes much bigger than necessary. This overwelding can have a tremendous impact on cost. To get an idea of how much you can read: Cost of Overwelding.

Having a basic understanding of how to properly size welds will equip you to question the size of certain welds. We are not telling you to go out and reduce all weld sizes immediately. Any change of this magnitude must be reviewed and approved by engineering. However, the savings can be significant.

To explain how to determine the strength of a weld we will use a simple example. In this article we will discuss only how to determine the strength of a transverse fillet weld. A transverse fillet weld is one that is perpendicular to the force applied as seen in the image below.

Because the load is perpendicular to the weld it is considered a tensile load. The formula we need to use to determine the load carrying capacity of the weld is:

Where

Fillet Weld Effective Throat

σt is the tensile strength of the weld (determined by the filler metal being used) in PSI

F is the force the weld can handle, in other words, the strength of the weld in lbf

A is the effective area of the weld

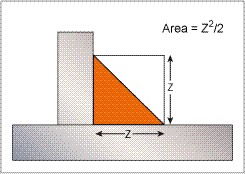
The effective area of a weld is calculated by multiplying the length of the weld times the throat of the weld. For design purposes we use the theoretical throat as shown below.

In the above diagram, is the fillet weld leg size. The theoretical throat is calculated by multiplying times the cosine of 45˚ which is 0.707. For all fillet welds with both legs being of the same size, the theoretical throat will be 0.707 x .

If the weld is 20 inches in length then the effective area will be 20 x 0.707 x .

Keeping with our example, there are two welds joining the two members. Both welds have a leg size of ¼-in and are 20 inches in length. We want to determine the maximum load these welds can withstand. The welding is being done with an ER70S-6 GMAW wire with minimum tensile strength of 70,000 psi.

First, determine the throat size.

Throat = x cos 45˚ = (1/4) x (0.707) = 0.177”

Now determine the effective area of the weld. Remember, there are two 20-inch long welds.

Effective Area = 2 x length x throat = (2) x (20) x (0.177) = 7.08 sq-in

Now we go back to our main formula.

Because we are using an ER70S-6 wire, is equal to 70,000 psi. Now we have all the values except for the one we are solving for, F.

We rearrange the formula to solve for F.

F = (70,000) x (7.08) = 495,600 lbf

So our 20-inch long, double-sided, ¼” fillet welds have a load carrying capacity able to withstand a tensile force of almost half a million pounds. To put this in perspective, a Boeing 747-400 weighs roughly 404,600 pounds. So, our seemingly tiny welds can pick up a 747! That is pretty impressive. However, before you go to the airport and put this to the test there are a few things you should know.

• If the force is applied rapidly the weld would fail at a significantly lower load
• If the force is not applied perfectly evenly along both welds the welds would fail at a significantly lower load
• If there are any weld discontinuities such as cracks, craters on undercut, the welds would fail at a significantly lower load
• If the load is not perfectly static, the welds would fail at a significantly lower load
• If the load is not perfectly perpendicular to the welds, the welds would fail at a significantly lower load

The list of “ifs” keeps going. Because of this, welding codes introduce a factor of safety. Factors of safety are used to make sure we don’t overload structures. In our next post we’ll provide an example of fillet welds loaded in shear. This is basically the worst case scenario and limits the maximum force that can be applied to a weld before it fails. Most of the design is made with the assumption that fillet welds will be loaded in shear.

A word of caution: the above calculations are used to explain the theory behind weld design. It is a simplified example to illustrate certain design principles. Proper testing and approvals by engineering must be in place before any changes can be made to welds when a specific size has previously been determined.

Reference: Design of Welded Structures

Formulae_Index
NomenclatureWeld Strength Calculations

Introduction..... Relevant Standards..... Variables Associated With Welds.....
Guidance Principles..... Table Basic Weld Calcs...... Assessment of Fillet Welds.....
Examples of Fillet Welds Calcs..... Properties of Fillet Welds as lines.....
Example of torsion weld calc. using vectors..... Capacities of Fillet Welds..... Design Strength of Fillet Welds.....

Introduction The following notes are general guidance notes showing methods ofcalculation of the strength and size of welds. Welded joints are oftencrucially important affecting the safety of the design systems. It isimportant that the notes and data below are only used for preliminary designevaluations. Final detail design should be completed in a formal wayusing appropriate codes and standards and quality reference documents Relevant Standards BS 5950-1:2000 ..Structural use of steelwork in building. Code of practice for design. Rolled and welded sections BS EN 10025-1:2004 - Hot rolled products of structural steels. General technical delivery conditions Variables related to welded joints Strength of deposited weld material Type of joint and weld..important Size of weld ..important Location of weld in relation to parts joined..important Types of stress to which the weld is subjected Conditions under which weld is carried out Type of equipment used for welding Skill of welder Guidance Principles A generous factor of safety should be used (3-5) and if fluctuatingloads are present then additional design margins should be included to allow for fatigue Use the minimum amount of filler material consistent with the job requirement Try to design joint such that load path is not not through the weld The table below provides provides approximate stresses in, hopefully, a convenientway. For the direct loading case the butt weld stresses are tensile/ compressive σ t for the fillet weldsthe stresses are assumed to be shear τ s applied to the weld throat. For butt welded joints subject to bending the butt weld stresses result from a tensile/compressive stress σb and a direct shearstress τ s . In these cases the design basis stress should be σr = Sqrt (σb2 + 4τs2) For Fillet welded joints subject to bending the stresses in the fillet welds are all shear stresses. From bending τ b and from shear τ s In these cases the design basis stress is generally τr =Sqrt (τ b2 + τs2) The stresses from joints subject to torsion loading include shear stress from the applied loadand shear stresses from the torque loading. The resulting stresses should be addedvectorially taking care to choose the location of the highest stresses. Table of bracket weld subject to direct and bending stresses Method of Loading Weldment Stress in Weld σb τs Weld size (h) Weldment Stress in Weld σb τs Weld size (h) Weldment Stress in Weld τb τs Weld size (h) Assessment of Fillet Weld Groups ref notes and table Properties of Fillet Welds as lines Important note: The methods described below is based on the simple method of calculationof weld stress as identified in BS 5950- clause 6.7.8.2 . The other method identifed in BS 5950 - 1 clause 6.7.8.3as the direction method uses the method of resolving the forces transmittedby unit thickness welds per unit length into traverse forces (FT ) andlongitudinal forces (FL ). I have, to some extent,illustrated this method in my examples below The method of assessing fillet welds groups treating welds as lines is reasonablysafe and conservative and is very convenient to use. a) Weld subject to bending....See table below for typical unit areas and unit Moments of Inertia A fillet weld subject to bending is easily assessed as follows. 1) The area of the fillet weld A u..(unit thickness) is calculated assuming the weldis one unit thick.. 2) The (unit) Moment of Inertia I u is calculated assuming the weldis one unit thick.. 3) The maximum shear stress due to bending is determined...τb = M.y/I u 4) The maximum shear stress due to direct shear is determined.. τs = P /A 5) The resultant stress τr = Sqrt (τb2 + τs2 ) 6) By comparing the design strength p w with the resultant stress τr the value of the weld throat thickness is calculated and then the weld size. i.e. if the τr /p w = 5 then the throat thickess t = 5 unitsand the weld leg size h = 1,414t a) Weld subject to torsion...See table below for typical unit areas and unit Polar moments of Inertia A fillet weld subject to torsion is easily assessed as follows. 1) The area of the fillet weld A u (unit thickness) is calculated assuming the weldis one unit thick 2) The (unit) Polar Moment of Inertia J u is calculated assuming the weldis one unit thick.. The polar moment of inertia J = I xx + I yy 3) The maximum shear stress due to torsion is determined...τt = T.r/J u 4) The maximum shear stress due to direct shear is determined.. τs = P /A u 5) The resultant stress τr is the vector sum of τt and τs. r is chosen to givethe highest value of τr 6) By comparing the design strength p w with the resultant stress τr the value of the weld throat thickness is calculated and then the weld size. i.e. if the τr /p w = 5 then the throat thickess t = 5 unitsand the weld leg size h = 1,414.t Examples of Fillet Weld Calculations Example of Weld in Torsion..P = Applied load = 10 000N P w = Design Strength = 220 N/mm 2 (Electrode E35 steel S275) Design Strength b = 120mm. d = 150 mm x = b2 / 2(b+d) = 27mm.. (From table below) y = d2 / 2(b+d) = 42mm..(From table below) Simple Method as BS 5950 clause 6.8.7.2 ..The vector sum of the stresses due to forces and moments should not exceed the designstrength Pw A u = Unit Throat Area = (From table below) b + d = (120 + 150) = 270mm2 To obtain radius of Force from weld centre of gravity A = 250-27 =223mm Moment M = P.r = 10000.223 = 2,23.106 N.mm J u = [(b+d)4 - 6b2d2] /12 (b+d) = 1,04.106..(From Table) It is necessary to locate the point subject to the highest shear stress..For a weld subject to only torsionthis would be simply at the point furthest from the COG. However because the weld is subject totorsion and direct shear the problem is more complicated. A normal method ofdetermining the stresses in these cases is to use vector addition. It is generally prudent to calculate the total shear stress at both positions, using the method below,and select the highest.. For this example the method used is to resolve the stressesin the x and y directions First considering point Z Horizontal distance from centroid r zh = 120-27= 93mm Vertical distance from centroid r zv = 42mm The vertical stress τv = τsv + τtv τsv = P /A u = 10000/270 = 37 N/mm2 τtv = M.r zh /J u = 2,23.106.93/1,04.106 = 199 N/mm2 τv = 236,45 N/mm2 The horizontal stress τh = τsh + τth τsh = 0 τth = M.r zv /J u = 2,23.106.42/1,04.106 = 90 N/mm2 τh = 90 N/mm2 The resultant stress on the weld at z τr = Sqrt (τh2 + τv2) = 253 N/mm2 Now considering point w Horizontal distance from centroid r wh = 27mm Vertical distance from centroid r wv = 150-42= 108mm The vertical stress τv = τsv - τtv τsv = P /A u = 10000/270 = 37 N/mm2 τtv = M.r wh /J u = 2,23.106.27/1,04.106 = 57,9 N/mm2 τv = 20,86 N/mm2 The horizontal stress τh = τsh + τth τsh = 0 τth = T.r wv /J u = 2,23.106.108/1,04.106 = 231,6 N/mm2 τh = 231,6 N/mm2 The resultant stress on the weld at w τr = Sqrt (τh2 + τv2) = 232,5 N/mm2 The maximum stress is similar but greatest at z .... The design strength p w for the weld material is 220 N/mm 2 The weld throat thicknessshould be 253 /220 = 1,15mm . The weld size is therefore 1,414. 1,15 = 1,62mm use 3mm fillet weld Direction Method as BS 5950 clause 6.8.7.3 L = Length of weld 1 unit thick = (From table below) b + d = (120 + 150) = 270mm To obtain radius of Force from weld Centre of Gravity (Cog) . A = 250-27 =223mm Moment M = P.r = 10000.223 = 2,23.106 N.mm Ju = Polar Moment of inertia for weld 1unit(mm) thick. = [(b+d)4 - 6b2d2] /12 (b+d) = 1,04.106 mm4 /mm..(From Table) It is necessary to locate the point subject to the highest shear stress..For a weld subject to only torsionthis would be simply at the point furthest from the COG. However because the weld is subject totorsion and direct shear the problem is more complicated. A normal method ofdetermining the stresses in these cases is to use vector addition. It is generally prudent to calculate the total shear stress at both positions, using the method below,and select the highest.. For this example the method used is to resolve the stressesin the x and y directions First considering point Z Horizontal distance from centroid r zh = 120-27= 93mm Vertical distance from centroid r zv = 42mm The vertical force /mm run F v = F sv + F tv F sv = P /L = 10000/270 = 37 N/mm run F tv = M.r zh /J u = 2,23.106.93/1,04.106 = 199 N/mm run F v = 236,45 N/mm run The horizontal force /mm run for unit(mm) weld width F h = F sh + F th F sh = 0 F th = M.r zv /J u = 2,23.106.42/1,04.106 = 90 N/mm run F h = 90 N/mm run The resultant force on the weld/mm run at z F r= Sqrt (F h2 + F v2)= 253 N/mm run Now considering point w Horizontal distance from centroid r wh = 27mm Vertical distance from centroid r wv = 150-42= 108mm The vertical forces per mm run F v = F sv - F tv F sv = P /L = 10000/270 = 37 N/mm run F tv = M.r wh /J u = 2,23.106.27/1,04.106 = 57,9 N/mm run F v = 20,86 N/mm run The horizontal force /mm run = F h = F sh + F th F sh = 0 F th = M.r wv /J u = 2,23.106.108/1,04.106 = 231,6 N/mm run F h = 231,6 N/mm run The specific force on the weld at w F r = Sqrt (F h2 + F v2) = 232,5 N/mm run The maximum specific is greatest at z = 253 N/mm run.... Referring to weld capacities for longitudinal stresses PL for fillet welds Capacities of Fillet Weldsthe weld capacity for a 3mm weld with and E35 Electrode S275 Steel is 462N /mm run. This weld would be more than sufficient. Example of Weld in Bending..P= 30000 Newtons d= 100mm b= 75mm y = 50mm Design Stress p w = 220 N/mm 2 (Electrode E35 steel S275) Design Strength Moment = M = 30000*60=18.10 5 Nmm Simple Method as BS 5950 clause 6.8.7.2 Unit Weld Area = A u = 2(d+b) =2(100+75) =350mm 2 Unit Moment of Inertia = I u = d 2(3b+d) / 6 = 100 2 (3.75 +100) / 6 =5,42.105mm4 τr = Sqrt(τs2 + τb2) τs = P / A u = 30000/350 = 85,71 N/mm 2 τb = M.y / I u = 18.105 . 50 / 5,42.105 = 166,05 N/mm 2 τr = Sqrt(85,71 2 + 166.052) =186,86 N/mm2 τr / p w = 186,86 / 220 = 0,85 = Throat Thickness..... ( Throat thickness for τ< />< sub=' /> = 220 N/mm2 ) Leg Length = Throat thickness *1,414 = 1,2mm use 3mm weld thickness Note : If a leg length h= 1,2mm is used in the equations in relevantpart of the 'Table of bracket weld subject to direct and bending stresses' abovea value of τb = 198 N/mm and a valueof τs = 100 N/mm2 results with a resultantstress of Sqrt (τ b2 + τs2)= 222N/mm2..Which is in generalagreement with the above result < /> Direction Method as BS 5950 clause 6.8.7.3 Length of Weld of unit thickness = L = 2(d+b) =2(100+75) =350mm Moment of Inertia / mm throat thickness = I u / mm = d 2(3b+d) / 6= 100 2 (3.75 +100) / 6 =5,42.105mm 4 / mm F r = Resultant force per unit length of weld. F s = Shear force per unit length of weld. F b = Bending force per unit length of weld. F r = Sqrt(F s2 + F b2) F s = P / L = 30000/350 = 85,71 N per mm length of weld F b = M.y / I u = 18.105 . 50 / 5,42.105 = 166,05 N per mm length of weld F r = Sqrt(85,71 2 + 166.052) =186,86 N per mm length of weld. For this case for the welds under greatest loading the type of loading is traverse loading.The bending stress is in line with horizontal element and the shear stress is in line with vertical member. The angle of the resulting specific load to the horizontal element = arctan(85,71/166,5)= 27,5o. This is an angle with the weld throat θ = 45o + 27,5o = 72,5oReferring to weld capacities table below.Weld Capacities K is calculated at 1,36 for this resultant direction of forces. PT = a.K.pwfor a E35 Weld electrodeused with S275 steel pw = 220 N/mm2 and therefore PT = a*300N/mm2.. A 3mm weld (a = 2,1mm) therefore will therefore have a design capacity of 630 N/mm run and will easily be able tosupport the load of 186,86 N per mm run Properties of weld groups with welds treated as lines - It is accepted that it is reasonably accurate to use properties based onunit weld thickness in calculation to determine the strength of welds as shown in the examples onthis page. The weld properties Ixx Iyy and J are assumedto be proportional to the weld thickness. The typical accuracy of this method ofcalculation is shown below... This is illustrated in the tabled values below d b h Ixx Iyy J= Ixx +Iyy Accurate 3 60 50 955080 108000 1063080 Simple 3 60 50 900000 108000 1008000 Error 6% 0 5% Note: The error identified with this method is lower as h increasesrelative to d. This error is such that the resulting designs are conservative. Example illustrating use of stress vectors Calculations based on unit values This calculation uses equations from table below for Area, centroid, and Ju 1) Area of weld = 0,707.5.(2b+d) Area = 0,707.5.(2.55 + 50) = 565.6mm2 2) There is no need to calculate the Moment of Area with this method 3) The centroid v = b2 /(2b+d) v = 552/(2.55+50)= 18,9mm 4) The radii rA, rB, rC & rD are calculated .. rA = rB = Sqrt ((55-18,9)^2 + 25^2 ) = 43,9 rC = rD = Sqrt (18,9^2 + 25^2 ) = 31,34 5) The angles θA, θB, θC & θD are calculated .. θA = θB = tan-1 ((55-18,9)/ 25 ) = 55,29o θC = θD = tan-1 ((18,9)/25 ) = 37o... 6) The direct shear stress on the area = Force /Area τ S = 5000/565,5 = 8,84 N/mm2 7) The Moment on the weld group = Force .distance to centroid M = 5000.(100+18,9) = 5.94.105Nmm 8) The Unit Polar moment of inertia of the weld group = Ju = 0.707.5.(8.b3 +6bd2+d3)/12 + b4/(2b+d) Ju = 0,707.5.(8.553+6.55.502 + 503)/12 - 553/(2.55+50) = 4,69.105 9) The stress due to torsion τ TA =τ TB = M.rA/J.. and ..τ TC =τ TD = M.rC/J τ TA = 5,94.105Nmm.43,9mm / 4,69.105mm4=55,6 N/mm2 τ TC = τ TD = 5,945Nmm.31,34mm / 4,69.105mm4= 39,69N/mm2 10) The resultant stresses τ RA, = τ RB and τ RA, = τ RB are obtainedby adding the stress vectos graphically as shown below τ RA = τ RB=48,59 N/mm2 τ RC = τ RD = 45,56N/mm2 Note: The example above simply illustrates the vector method adding direct and torsional shear stresses and compares the differencein using the unit weld width method and using real weld sizes. The example calculates the stress levels in an existing weld groupit is clear that the weld is oversized for the loading scenario. The difference in the resulting values are in less than 4%. If the welds were smalleri.e 3mm then the differences would be even smaller. Table properties of a range of fillet weld groups with welds treated as lines - Weld Throat Area Unit Area Location of COG x y I xx-(unit) J-(Unit) - - Table Of Weld Capacities The fillet weld capacity tables related to the type of loading on the weld. Twotypes of loading are identified traverse loading and longitudinal loading as show below The weld loading should be such that { (FL/PL) 2 + (FT/PT) 2 } ≤ 1 The following table is in accord with data in BS 5950 part 1. Based ondesign strengths as shown in table below ... Design Strength PL = a.pw PT = a.K.pw a = weld throat size. K =1,25 √ (1,5 / (1 + Cos 2θ ) PT based on elements transmitting forces at 90o i.e θ = 45o and K = 1,25 Weld Capacity E35 Electrode S275 Steel Weld Capacity E42 Electrode S355 Steel Leg Length Throat Thickness Longitudinal Capacity Transverse Capacity Leg Length Throat Thickness Longitudinal Capacity Transverse Capacity P L(kN/mm) P T (kN/mm) P L P T mm mm kN/mm kN/mm mm mm kN/mm kN/mm 3 2,1 0,462 0,577 3 2,1 0,525 0,656 4 2,8 0,616 0,720 4 2,8 0,700 0,875 5 3,5 0,770 0,963 5 3,5 0,875 1,094 6 4,2 0,924 1,155 6 4,2 1,050 1,312 8 5,6 1,232 1,540 8 5,6 1,400 1,750 10 7,0 1,540 1,925 10 7,0 1,750 2,188 12 8,4 1,848 2,310 12 8,4 2,100 2,625 15 10,5 2,310 2,888 15 10,5 2,625 3,281 18 12,6 2,772 3,465 18 12,6 3,150 3,938 20 14,0 3,08 3,850 20 14,0 3,500 4,375 22 15,4 3,388 4,235 22 15,4 3,850 4,813 25 17,5 3,850 4,813 25 17,5 4,375 5,469 Design Strength p w of fillet welds Electrode classification Steel Grade 35 43 50 N/mm2 N/mm2 N/mm2 S275 220 220 220 S355 220 250 250 S460 220 250 280

Useful Related Links Gowelding..A Real Find..this site has lots ofInformation on calculating the strength of Welds Weld Design Notes ..A set of excellent design notes

Formulae_Index

Weld Throat Thickness Calculation

Nomenclature